Olivier Brunet

Data Geek :)

7 minute read

California Housing Prices

Prediction of Median house prices for California districts derived from the 1990 census.

Header by Vita Vilcina

Context

This is the dataset used in the second chapter of Aurélien Géron’s recent book ‘Hands-On Machine learning with Scikit-Learn and TensorFlow’. It serves as an excellent introduction to implementing machine learning algorithms because it requires rudimentary data cleaning, has an easily understandable list of variables and sits at an optimal size between being to toyish and too cumbersome.

The data contains information from the 1990 California census. So although it may not help you with predicting current housing prices like the Zillow Zestimate dataset, it does provide an accessible introductory dataset for teaching people about the basics of machine learning.

Acknowledgements

Please refer to the Kaggle challenge web page

Inspiration

predict a real estate price

Exploratory Data Analysis

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import os

import folium

from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error 
from sklearn.linear_model import Lasso, LinearRegression, Ridge, RANSACRegressor, SGDRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn.svm import SVR

file_path = os.path.join('input', 'house_big.csv')
df = pd.read_csv(file_path)
df.head()
longitude latitude housing_median_age total_rooms total_bedrooms population households median_income median_house_value ocean_proximity
0 -122.23 37.88 41.0 880.0 129.0 322.0 126.0 8.3252 452600.0 NEAR BAY
1 -122.22 37.86 21.0 7099.0 1106.0 2401.0 1138.0 8.3014 358500.0 NEAR BAY
2 -122.24 37.85 52.0 1467.0 190.0 496.0 177.0 7.2574 352100.0 NEAR BAY
3 -122.25 37.85 52.0 1274.0 235.0 558.0 219.0 5.6431 341300.0 NEAR BAY
4 -122.25 37.85 52.0 1627.0 280.0 565.0 259.0 3.8462 342200.0 NEAR BAY 
df.shape

(20640, 10)

Content

The data pertains to the houses found in a given California district and some summary stats about them based on the 1990 census data. Be warned the data aren’t cleaned so there are some preprocessing steps required! The columns are as follows, their names are pretty self explanitory:

  • longitude
  • latitude
  • housing_median_age
  • total_rooms
  • total_bedrooms
  • population
  • households
  • median_income
  • median_house_value
  • ocean_proximity
df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
longitude             20640 non-null float64
latitude              20640 non-null float64
housing_median_age    20640 non-null float64
total_rooms           20640 non-null float64
total_bedrooms        20433 non-null float64
population            20640 non-null float64
households            20640 non-null float64
median_income         20640 non-null float64
median_house_value    20640 non-null float64
ocean_proximity       20640 non-null object
dtypes: float64(9), object(1)
memory usage: 1.6+ MB

There are few missing value int the ‘total_bedrooms’ column. Now let’s see the basic stats for the numerical columns:

df.describe()
longitude latitude housing_median_age total_rooms total_bedrooms population households median_income median_house_value
count 20640.000000 20640.000000 20640.000000 20640.000000 20433.000000 20640.000000 20640.000000 20640.000000 20640.000000
mean -119.569704 35.631861 28.639486 2635.763081 537.870553 1425.476744 499.539680 3.870671 206855.816909
std 2.003532 2.135952 12.585558 2181.615252 421.385070 1132.462122 382.329753 1.899822 115395.615874
min -124.350000 32.540000 1.000000 2.000000 1.000000 3.000000 1.000000 0.499900 14999.000000
25% -121.800000 33.930000 18.000000 1447.750000 296.000000 787.000000 280.000000 2.563400 119600.000000
50% -118.490000 34.260000 29.000000 2127.000000 435.000000 1166.000000 409.000000 3.534800 179700.000000
75% -118.010000 37.710000 37.000000 3148.000000 647.000000 1725.000000 605.000000 4.743250 264725.000000
max -114.310000 41.950000 52.000000 39320.000000 6445.000000 35682.000000 6082.000000 15.000100 500001.000000 
df.ocean_proximity.value_counts()

<1H OCEAN     9136
INLAND        6551
NEAR OCEAN    2658
NEAR BAY      2290
ISLAND           5
Name: ocean_proximity, dtype: int64

Cleaning data

df.duplicated().sum()

0

df.isnull().sum()

longitude               0
latitude                0
housing_median_age      0
total_rooms             0
total_bedrooms        207
population              0
households              0
median_income           0
median_house_value      0
ocean_proximity         0
dtype: int64

print(f'percentage of missing values: {df.total_bedrooms.isnull().sum() / df.shape[0] * 100 :.2f}%')

percentage of missing values: 1.00%

df = df.fillna(df.median())
df.isnull().sum()

longitude             0
latitude              0
housing_median_age    0
total_rooms           0
total_bedrooms        0
population            0
households            0
median_income         0
median_house_value    0
ocean_proximity       0
dtype: int64

Dealing with geospatial infos

Visualization of the data in a scatter plot in a “geographic way”

sns.scatterplot(df.longitude, df.latitude)

<matplotlib.axes._subplots.AxesSubplot at 0x7f244cbecb00>

png

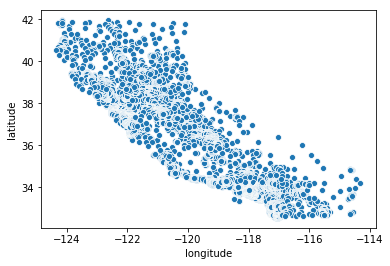
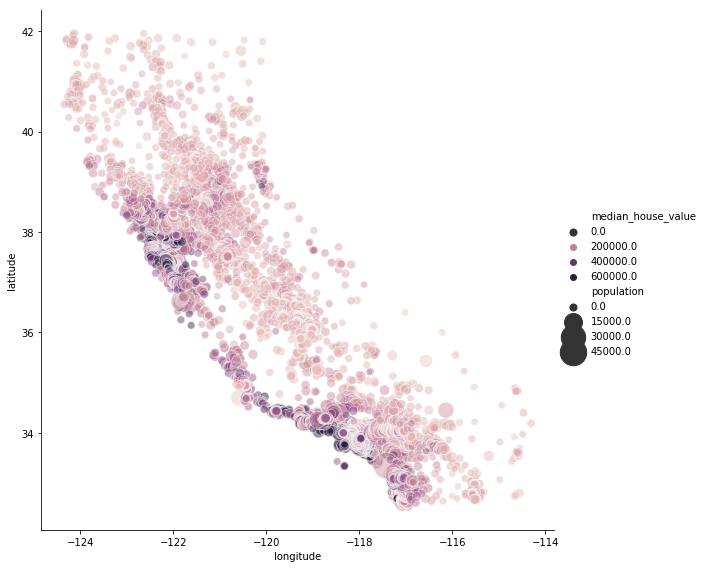
Same plot but this time with a varying size of the data points based on population variable and a different color depending of the real estate price (median_house_value)

sns.relplot(x="longitude", y="latitude", hue="median_house_value", size="population", alpha=.5,\
            sizes=(50, 700), data=df, height=8)
plt.show()

png

# Create a map with folium centered at the mean latitude and longitude
cali_map = folium.Map(location=[35.6, -117], zoom_start=6)

# Display the map
display(cali_map)

# Add markers for each rows
for i in range(df.shape[0]):
    folium.Marker((float(df.iloc[i, 1]), float(df.iloc[i, 0]))).add_to(cali_map) 
    
# Display the map
display(cali_map)

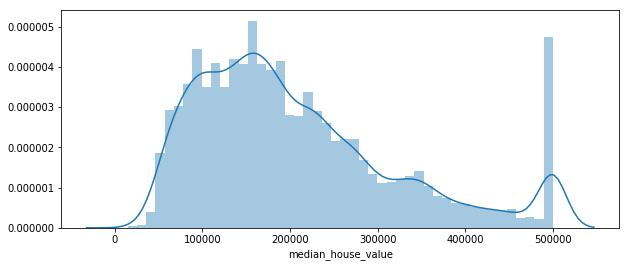
Target analysis

plt.figure(figsize=(10, 4))
sns.distplot(df.median_house_value)
plt.show()

/home/sunflowa/anaconda3/lib/python3.7/site-packages/scipy/stats/stats.py:1713: FutureWarning: Using a non-tuple sequence for multidimensional indexing is deprecated; use `arr[tuple(seq)]` instead of `arr[seq]`. In the future this will be interpreted as an array index, `arr[np.array(seq)]`, which will result either in an error or a different result.
  return np.add.reduce(sorted[indexer] * weights, axis=axis) / sumval

png

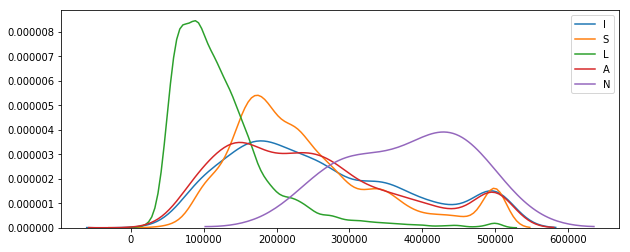
Variations depending on the proximity with ocean

df.ocean_proximity.unique()

array(['NEAR BAY', '<1H OCEAN', 'INLAND', 'NEAR OCEAN', 'ISLAND'],
      dtype=object)

plt.figure(figsize=(10, 4))
for prox in df.ocean_proximity.unique():
    sns.kdeplot(data=df[df.ocean_proximity == prox].median_house_value)
    plt.legend(prox)
plt.show()

png

Other analysis

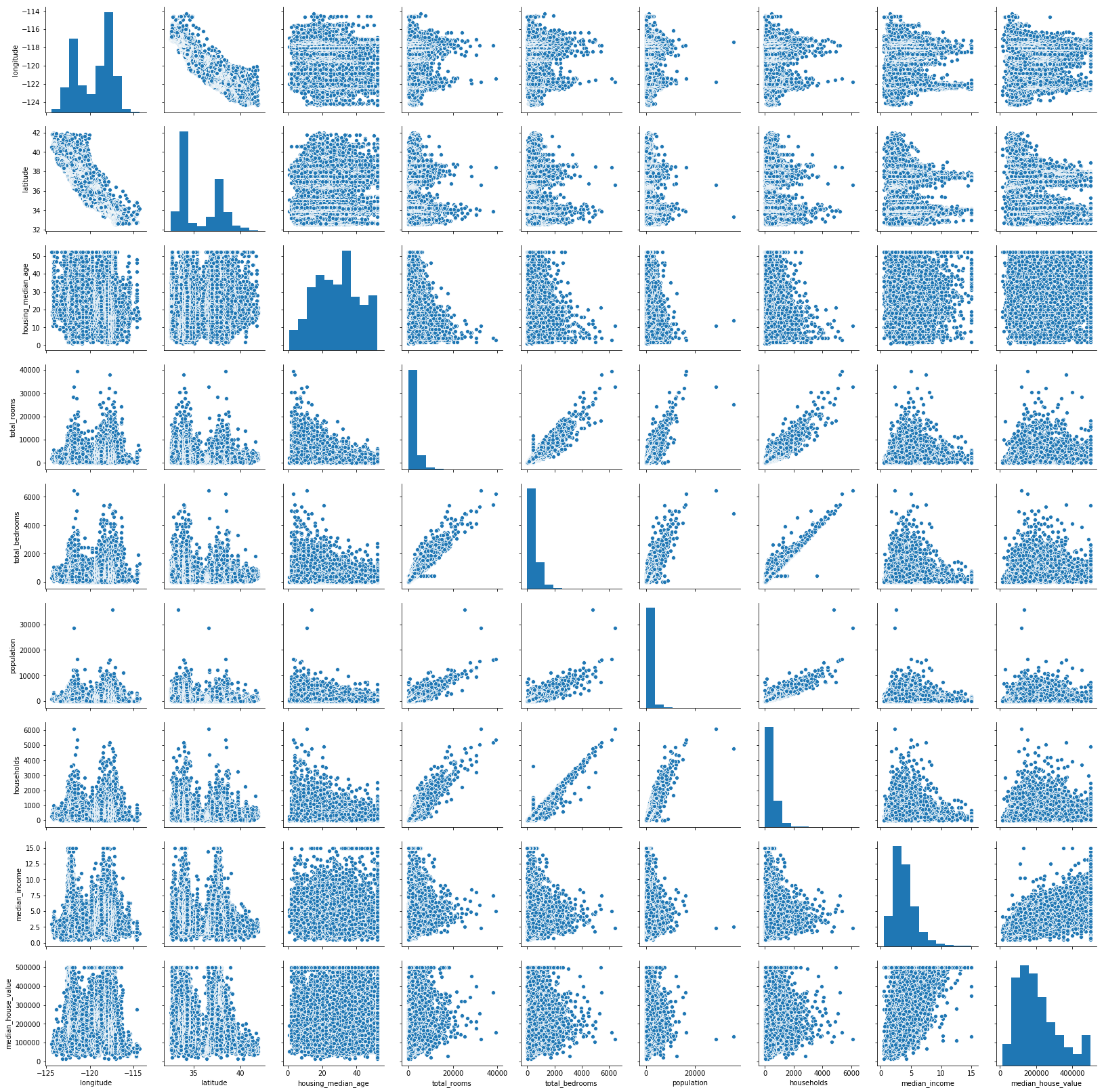
sns.pairplot(df)
plt.show()

png

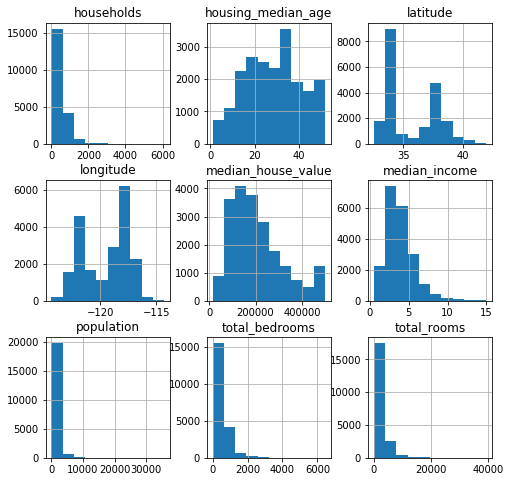
df.hist(figsize=(8, 8))
plt.show()

png

Correlations

corr = df.corr()
corr
longitude latitude housing_median_age total_rooms total_bedrooms population households median_income median_house_value
longitude 1.000000 -0.924664 -0.108197 0.044568 0.069120 0.099773 0.055310 -0.015176 -0.045967
latitude -0.924664 1.000000 0.011173 -0.036100 -0.066484 -0.108785 -0.071035 -0.079809 -0.144160
housing_median_age -0.108197 0.011173 1.000000 -0.361262 -0.319026 -0.296244 -0.302916 -0.119034 0.105623
total_rooms 0.044568 -0.036100 -0.361262 1.000000 0.927058 0.857126 0.918484 0.198050 0.134153
total_bedrooms 0.069120 -0.066484 -0.319026 0.927058 1.000000 0.873535 0.974366 -0.007617 0.049457
population 0.099773 -0.108785 -0.296244 0.857126 0.873535 1.000000 0.907222 0.004834 -0.024650
households 0.055310 -0.071035 -0.302916 0.918484 0.974366 0.907222 1.000000 0.013033 0.065843
median_income -0.015176 -0.079809 -0.119034 0.198050 -0.007617 0.004834 0.013033 1.000000 0.688075
median_house_value -0.045967 -0.144160 0.105623 0.134153 0.049457 -0.024650 0.065843 0.688075 1.000000 
# Generate a mask for the upper triangle
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True

# Set up the matplotlib figure
f, ax = plt.subplots(figsize=(8, 6))

# Generate a custom diverging colormap
cmap = sns.diverging_palette(220, 10, as_cmap=True)

# Draw the heatmap with the mask and correct aspect ratio
sns.heatmap(corr, mask=mask, cmap=cmap, vmax=.3, center=0,
            square=True, linewidths=.5, cbar_kws={"shrink": .5}, annot=True)

<matplotlib.axes._subplots.AxesSubplot at 0x7f243ec37898>

png

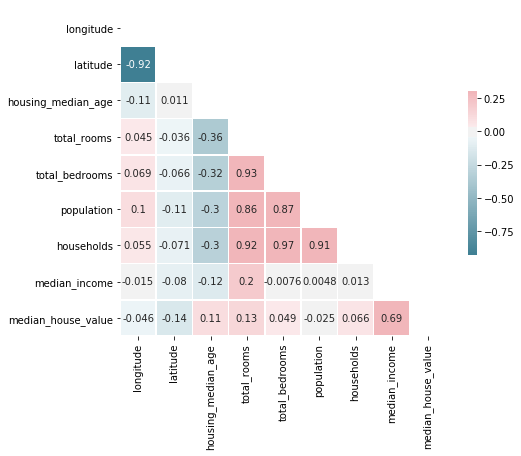
  • lat and log are highly positively correlated
  • total_bedrooms, population and householdsare highly positively correlated too
  • median_income and median_house_value are also positively correlated

which make sense.

Models training and predictions

Data preparation

Label encoding of categorical feature (ocean proximity)

df = pd.get_dummies(data=df, columns=['ocean_proximity'], drop_first=False)
df.head()
longitude latitude housing_median_age total_rooms total_bedrooms population households median_income median_house_value ocean_proximity_<1H OCEAN ocean_proximity_INLAND ocean_proximity_ISLAND ocean_proximity_NEAR BAY ocean_proximity_NEAR OCEAN
0 -122.23 37.88 41.0 880.0 129.0 322.0 126.0 8.3252 452600.0 0 0 0 1 0
1 -122.22 37.86 21.0 7099.0 1106.0 2401.0 1138.0 8.3014 358500.0 0 0 0 1 0
2 -122.24 37.85 52.0 1467.0 190.0 496.0 177.0 7.2574 352100.0 0 0 0 1 0
3 -122.25 37.85 52.0 1274.0 235.0 558.0 219.0 5.6431 341300.0 0 0 0 1 0
4 -122.25 37.85 52.0 1627.0 280.0 565.0 259.0 3.8462 342200.0 0 0 0 1 0 
feat_removed = ['median_house_value']

# removed 
#['longitude', 'latitude', 'housing_median_age', 'total_rooms', 'total_bedrooms', 'population', 'households', 'median_income',
#'median_house_value', 'ocean_proximity']

y = df.median_house_value
X = df.drop(columns=feat_removed)
X.shape, y.shape

((20640, 13), (20640,))

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

Metric RMSE root mean squared error

Root Mean Square Error (RMSE) is the standard deviation of the residuals (prediction errors). Residuals are a measure of how far from the regression line data points are; RMSE is a measure of how spread out these residuals are. In other words, it tells you how concentrated the data is around the line of best fit. Root mean square error is commonly used in climatology, forecasting, and regression analysis to verify experimental results.

def calculate_rmse(model, model_name):
    model.fit(X_train, y_train)
    y_pred, y_pred_train = model.predict(X_test), model.predict(X_train)
    rmse_test, rmse_train = np.sqrt(mean_squared_error(y_test, y_pred)), np.sqrt(mean_squared_error(y_train, y_pred_train))
    print(model_name, f' RMSE on train: {rmse_train:.0f}, on test: {rmse_test:.0f}')
    return rmse_test

Linear Regression

lr = LinearRegression()
lr_err = calculate_rmse(lr, 'Linear Reg')

Linear Reg  RMSE on train: 68533, on test: 69932

RANSAC Regressor

ra = RANSACRegressor()
ra_err = calculate_rmse(ra, 'RANSAC Reg')

RANSAC Reg  RMSE on train: 78281, on test: 78795

Lasso

la = Lasso()
la_err = calculate_rmse(la, 'Lasso Reg')

Lasso Reg  RMSE on train: 68533, on test: 69932


/home/sunflowa/anaconda3/lib/python3.7/site-packages/sklearn/linear_model/coordinate_descent.py:492: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations. Fitting data with very small alpha may cause precision problems.
  ConvergenceWarning)

SGD Regressor

sg = SGDRegressor()
sg_err = calculate_rmse(sg, 'SGD Reg')

SGD Reg  RMSE on train: 2939589866401599, on test: 2954302199978100


/home/sunflowa/anaconda3/lib/python3.7/site-packages/sklearn/linear_model/stochastic_gradient.py:166: FutureWarning: max_iter and tol parameters have been added in SGDRegressor in 0.19. If both are left unset, they default to max_iter=5 and tol=None. If tol is not None, max_iter defaults to max_iter=1000. From 0.21, default max_iter will be 1000, and default tol will be 1e-3.
  FutureWarning)

Ridge

ri = SGDRegressor()
ri_err = calculate_rmse(ri, 'Ridge')

Ridge  RMSE on train: 24125952802617160, on test: 24256192059939448


/home/sunflowa/anaconda3/lib/python3.7/site-packages/sklearn/linear_model/stochastic_gradient.py:166: FutureWarning: max_iter and tol parameters have been added in SGDRegressor in 0.19. If both are left unset, they default to max_iter=5 and tol=None. If tol is not None, max_iter defaults to max_iter=1000. From 0.21, default max_iter will be 1000, and default tol will be 1e-3.
  FutureWarning)

AdaBoostRegressor

ad = AdaBoostRegressor()
ad_err = calculate_rmse(ad, 'AdaBoostRegressor')

AdaBoostRegressor  RMSE on train: 86734, on test: 86345

SVR

sv = SVR()
sv_err = calculate_rmse(sv, 'SVR')

/home/sunflowa/anaconda3/lib/python3.7/site-packages/sklearn/svm/base.py:196: FutureWarning: The default value of gamma will change from 'auto' to 'scale' in version 0.22 to account better for unscaled features. Set gamma explicitly to 'auto' or 'scale' to avoid this warning.
  "avoid this warning.", FutureWarning)


SVR  RMSE on train: 118660, on test: 117282

Results comparison

df_score = pd.DataFrame({'Model':['Linear Reg', 'RANSAC Reg', 'Lasso Reg', 'AdaBoost', 'SVR'], 
                         'RMSE':[lr_err, ra_err, la_err, ad_err, sv_err]})
ax = df_score.plot.barh(y='RMSE', x='Model')

png

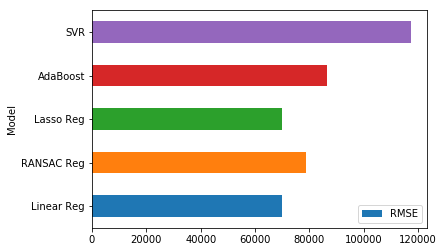
Lasso and the Linear Reg are the winners ! Surprisingly the RSME is a little lower for the best models when we keep features such as lat/long and ‘total_bedrooms’, ‘population’.

You May Also Enjoy

H&M Personalized Fashion 1/2 - EDA

11 minute read

Exploratory analysis of articles, customers, and transactions datasets with recommendation engine specific caracteristics, such as a long tail.

What is federated learning?

10 minute read

A sub-field of ML focusing on decentralization, motivated by issues such as data privacy, data minimization, and data access rights.