Forecast of city bikeshare system’s use / rentals

Banner photo by Christian Stahl

Context

Bike sharing systems are a means of renting bicycles where the process of obtaining membership, rental, and bike return is automated via a network of kiosk locations throughout a city. Using these systems, people are able rent a bike from a one location and return it to a different place on an as-needed basis. Currently, there are over 500 bike-sharing programs around the world.

The data generated by these systems makes them attractive for researchers because the duration of travel, departure location, arrival location, and time elapsed is explicitly recorded. Bike sharing systems therefore function as a sensor network, which can be used for studying mobility in a city. In this competition, participants are asked to combine historical usage patterns with weather data in order to forecast bike rental demand in the Capital Bikeshare program in Washington, D.C.

Goal

Forecast use of a city bikeshare system

---

Exploratory Data Analysis

import numpy as np
import pandas as pd
from scipy import stats
import seaborn as sns
import matplotlib.pyplot as plt

pd.options.display.max_columns = 100

import warnings
warnings.filterwarnings("ignore")

from sklearn.svm import LinearSVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression, Ridge, Lasso, ElasticNet
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor, ExtraTreesRegressor

from sklearn.model_selection import GridSearchCV
from sklearn import metrics
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, PolynomialFeatures

import xgboost as xgb
import lightgbm as lgbm

Let’s see the head of the data set

df = pd.read_csv("../input/train.csv")
df.head()

	datetime	season	holiday	workingday	weather	temp	atemp	humidity	windspeed	casual	registered	count
0	2011-01-01 00:00:00	1	0	0	1	9.84	14.395	81	0.0	3	13	16
1	2011-01-01 01:00:00	1	0	0	1	9.02	13.635	80	0.0	8	32	40
2	2011-01-01 02:00:00	1	0	0	1	9.02	13.635	80	0.0	5	27	32
3	2011-01-01 03:00:00	1	0	0	1	9.84	14.395	75	0.0	3	10	13
4	2011-01-01 04:00:00	1	0	0	1	9.84	14.395	75	0.0	0	1	1

The dataset contains the following columns:

datetime - hourly date + timestamp  
season -  1 = spring, 2 = summer, 3 = fall, 4 = winter 
holiday - whether the day is considered a holiday
workingday - whether the day is neither a weekend nor holiday
weather - 1: Clear, Few clouds, Partly cloudy, Partly cloudy 
2: Mist + Cloudy, Mist + Broken clouds, Mist + Few clouds, Mist 
3: Light Snow, Light Rain + Thunderstorm + Scattered clouds, Light Rain + Scattered clouds 
4: Heavy Rain + Ice Pallets + Thunderstorm + Mist, Snow + Fog 
temp - temperature in Celsius
atemp - "feels like" temperature in Celsius
humidity - relative humidity
windspeed - wind speed
casual - number of non-registered user rentals initiated
registered - number of registered user rentals initiated
count - number of total rentals

‘count’ is the target, all other columns are features.

The value of ‘count’ is equal to casual plus register

df.shape

(10886, 12)

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10886 entries, 0 to 10885
Data columns (total 12 columns):
datetime      10886 non-null object
season        10886 non-null int64
holiday       10886 non-null int64
workingday    10886 non-null int64
weather       10886 non-null int64
temp          10886 non-null float64
atemp         10886 non-null float64
humidity      10886 non-null int64
windspeed     10886 non-null float64
casual        10886 non-null int64
registered    10886 non-null int64
count         10886 non-null int64
dtypes: float64(3), int64(8), object(1)
memory usage: 1020.6+ KB

There are basiclly 3 types of data:

• data concerning the weather
• for time infos
• linked to the number of users

No Nan, it seems that there isn’t any missing value. All types seem to be corresponding to the meaning of the data except the ‘datetime’ column wich is an object not a pandas’ datetime Let’s see the basic statistics:

df.describe()

	season	holiday	workingday	weather	temp	atemp	humidity	windspeed	casual	registered	count
count	10886.000000	10886.000000	10886.000000	10886.000000	10886.00000	10886.000000	10886.000000	10886.000000	10886.000000	10886.000000	10886.000000
mean	2.506614	0.028569	0.680875	1.418427	20.23086	23.655084	61.886460	12.799395	36.021955	155.552177	191.574132
std	1.116174	0.166599	0.466159	0.633839	7.79159	8.474601	19.245033	8.164537	49.960477	151.039033	181.144454
min	1.000000	0.000000	0.000000	1.000000	0.82000	0.760000	0.000000	0.000000	0.000000	0.000000	1.000000
25%	2.000000	0.000000	0.000000	1.000000	13.94000	16.665000	47.000000	7.001500	4.000000	36.000000	42.000000
50%	3.000000	0.000000	1.000000	1.000000	20.50000	24.240000	62.000000	12.998000	17.000000	118.000000	145.000000
75%	4.000000	0.000000	1.000000	2.000000	26.24000	31.060000	77.000000	16.997900	49.000000	222.000000	284.000000
max	4.000000	1.000000	1.000000	4.000000	41.00000	45.455000	100.000000	56.996900	367.000000	886.000000	977.000000

At first glance, when we look at the temp / atemp min, it seems strange that no negative temperature is recorded…

Weather informations analysis

plt.figure(figsize=(8, 4))
sns.distplot(df.temp, bins=10, label='real temp.')
sns.distplot(df.atemp, bins=10, label='feels like temp.')
plt.legend()
plt.show()

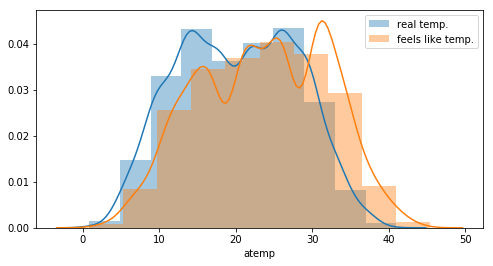
One can see an offset between the real temperature and the “feels like” temperature. This can probably explained by the fact that temperature on a bike is different. But the distributions looks the same. More, there is a clear correlation between the 2 features.

plt.figure(figsize=(4, 4))
sns.scatterplot(df.atemp, df.temp)
plt.show()

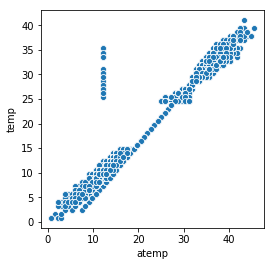
Let’s see if the difference between the 2 features is quite the same…

df['Delta'] = df.temp - df.atemp
sns.lineplot(x=df.index, y=df.Delta)

<matplotlib.axes._subplots.AxesSubplot at 0x7fa54c4cf588>

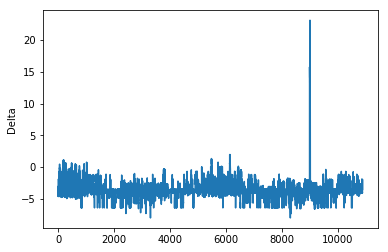
There are few abnormal values corresponding to the spike in the above plot.

df[df.Delta > 5].head()

	datetime	season	holiday	workingday	weather	temp	atemp	humidity	windspeed	casual	registered	count	Delta
8991	2012-08-17 00:00:00	3	0	1	1	27.88	12.12	57	11.0014	21	67	88	15.76
8992	2012-08-17 01:00:00	3	0	1	1	27.06	12.12	65	7.0015	16	38	54	14.94
8993	2012-08-17 02:00:00	3	0	1	1	27.06	12.12	61	8.9981	4	15	19	14.94
8994	2012-08-17 03:00:00	3	0	1	1	26.24	12.12	65	7.0015	0	6	6	14.12
8995	2012-08-17 04:00:00	3	0	1	1	26.24	12.12	73	11.0014	0	9	9	14.12

df[(df.atemp >= 12) & (df.atemp <= 12.5)].head()

	datetime	season	holiday	workingday	weather	temp	atemp	humidity	windspeed	casual	registered	count	Delta
59	2011-01-03 14:00:00	1	0	1	1	10.66	12.12	30	19.0012	11	66	77	-1.46
60	2011-01-03 15:00:00	1	0	1	1	10.66	12.12	30	16.9979	14	58	72	-1.46
61	2011-01-03 16:00:00	1	0	1	1	10.66	12.12	30	16.9979	9	67	76	-1.46
109	2011-01-05 18:00:00	1	0	1	1	9.84	12.12	38	8.9981	3	166	169	-2.28
115	2011-01-06 00:00:00	1	0	1	1	7.38	12.12	55	0.0000	0	11	11	-4.74

All those measures have been recorded the same day. During that day ‘temp’ changed but not ‘atemp’ The ‘atemp’ value seems strange even during other few days… Because those 2 features are correlated, we only need to keep one. This is more safe to keep temp instead of atemp

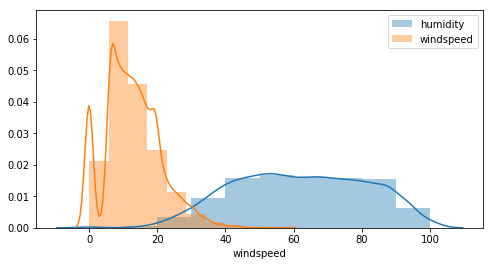
Is there also a correlation between humidity and windspeed ?

plt.figure(figsize=(8, 4))
sns.distplot(df.humidity, bins=10, label='humidity')
sns.distplot(df.windspeed, bins=10, label='windspeed')
plt.legend()
plt.show()

sns.pairplot(df[['temp', 'atemp', 'humidity', 'windspeed']])

<seaborn.axisgrid.PairGrid at 0x7fa547823a58>

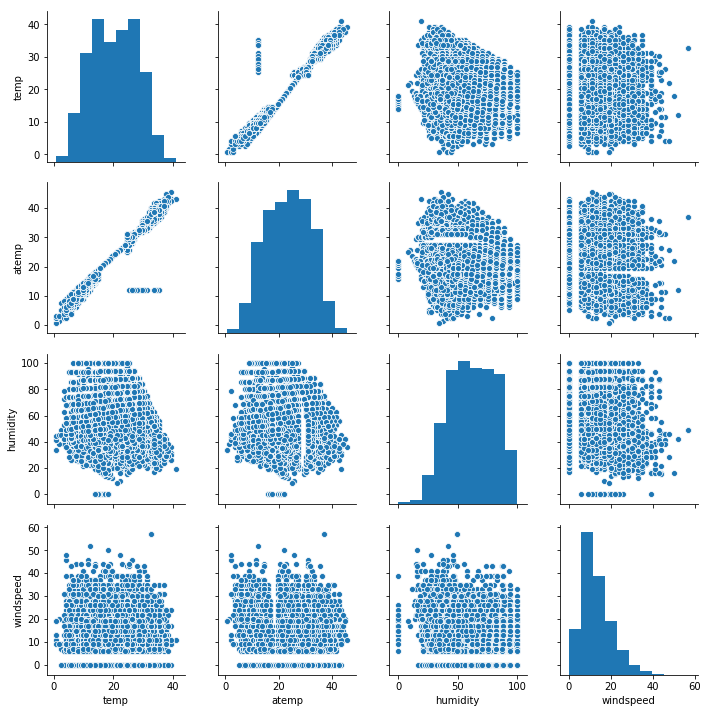
Except for the temperature, there is no clear correlation between other features. Furthermore:

• humidity vs atemp there is something strange with missing value like a void in the scatter
• for all windspeed plots there are null values and beginning values start at 5, that’s probably because the sensor can detect low values…this needs to be investigated further.

Modification of time data

df['casual_percentage'] = df['casual'] / df['count']
df['registered_percentage'] = df['registered'] / df['count']

def change_datetime(df):
    """ Modify the col datetime to create other cols: dow, month, week..."""
    df["datetime"] = pd.to_datetime(df["datetime"])
    df["dow"] = df["datetime"].dt.dayofweek
    df["month"] = df["datetime"].dt.month
    df["week"] = df["datetime"].dt.week
    df["hour"] = df["datetime"].dt.hour
    df["year"] = df["datetime"].dt.year
    df["season"] = df.season.map({1: "Winter", 2 : "Spring", 3 : "Summer", 4 :"Fall" })
    df["month_str"] = df.month.map({1: "Jan ", 2 : "Feb", 3 : "Mar", 4 : "Apr", 5: "May", 6: "Jun", 7: "Jul", 8: "Aug", 9: "Sep", 10: "Oct", 11: "Nov", 12: "Dec" })
    df["dow_str"] = df.dow.map({5: "Sat", 6 : "Sun", 0 : "Mon", 1 :"Tue", 2 : "Wed", 3 : "Thu", 4: "Fri" })
    df["weather_str"] = df.weather.map({1: "Good", 2 : "Normal", 3 : "Bad", 4 :"Very Bad"})
    return df
    
    
df = change_datetime(df)
df.head()

	datetime	season	holiday	workingday	weather	temp	atemp	humidity	windspeed	casual	registered	count	Delta	casual_percentage	registered_percentage	dow	month	week	hour	year	month_str	dow_str	weather_str
0	2011-01-01 00:00:00	Winter	0	0	1	9.84	14.395	81	0.0	3	13	16	-4.555	0.187500	0.812500	5	1	52	0	2011	Jan	Sat	Good
1	2011-01-01 01:00:00	Winter	0	0	1	9.02	13.635	80	0.0	8	32	40	-4.615	0.200000	0.800000	5	1	52	1	2011	Jan	Sat	Good
2	2011-01-01 02:00:00	Winter	0	0	1	9.02	13.635	80	0.0	5	27	32	-4.615	0.156250	0.843750	5	1	52	2	2011	Jan	Sat	Good
3	2011-01-01 03:00:00	Winter	0	0	1	9.84	14.395	75	0.0	3	10	13	-4.555	0.230769	0.769231	5	1	52	3	2011	Jan	Sat	Good
4	2011-01-01 04:00:00	Winter	0	0	1	9.84	14.395	75	0.0	0	1	1	-4.555	0.000000	1.000000	5	1	52	4	2011	Jan	Sat	Good

Rentals / target analysis

sns.kdeplot(data=df['count'])

<matplotlib.axes._subplots.AxesSubplot at 0x7fa5472d17b8>

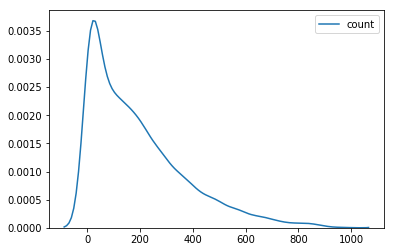
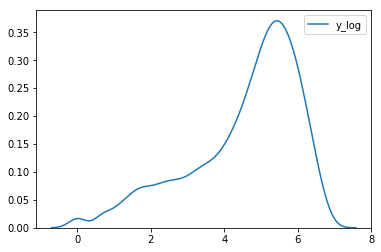
df['y_log'] = np.log(df['count'])
sns.kdeplot(data=df['y_log'])

<matplotlib.axes._subplots.AxesSubplot at 0x7fa5452d5e80>

plt.figure(figsize=(12, 6))
sns.pointplot(x=df["hour"], y=df["count"], hue=df["season"])
plt.xlabel("Hour Of The Day")
plt.ylabel("Users Count") 
plt.title("Rentals Across Hours")
plt.show()

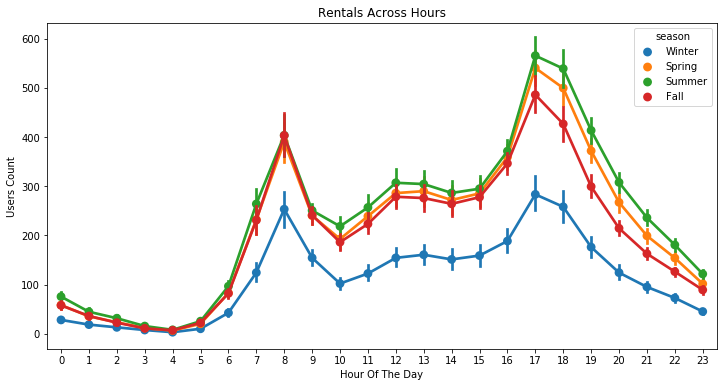
plt.figure(figsize=(12, 6))
sns.lineplot(x="hour", y="count", hue="season", data=df)

<matplotlib.axes._subplots.AxesSubplot at 0x7fa5452ca518>

# ---------------------------------------------------------
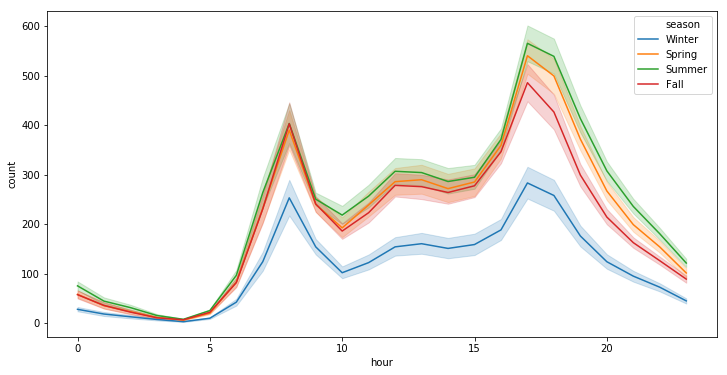
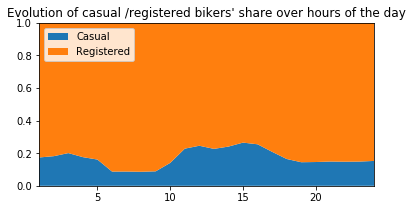
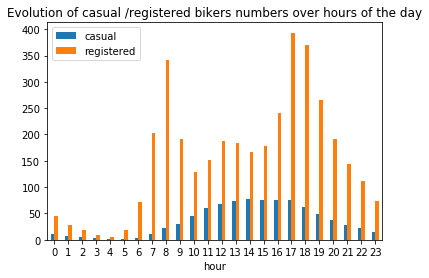
plt.figure(figsize=(6,3))
plt.stackplot(range(1,25),
              df.groupby(['hour'])['casual_percentage'].mean(), 
              df.groupby(['hour'])['registered_percentage'].mean(), 
              labels=['Casual','Registered'])
plt.legend(loc='upper left')
plt.margins(0,0)
plt.title("Evolution of casual /registered bikers' share over hours of the day")

# ---------------------------------------------------------
plt.figure(figsize=(6,6))
df_hours = pd.DataFrame(
    {"casual" : df.groupby(['hour'])['casual'].mean().values,
    "registered" : df.groupby(['hour'])['registered'].mean().values},
    index = df.groupby(['hour'])['casual'].mean().index)
df_hours.plot.bar(rot=0)
plt.title("Evolution of casual /registered bikers numbers over hours of the day")

# ---------------------------------------------------------
plt.show()

<Figure size 432x432 with 0 Axes>

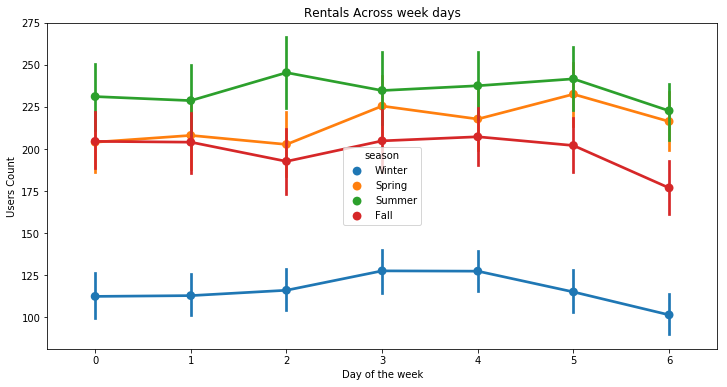
plt.figure(figsize=(12, 6))
sns.pointplot(x=df["dow"], y=df["count"], hue=df["season"])
plt.xlabel("Day of the week")
plt.ylabel("Users Count") 
plt.title("Rentals Across week days")
plt.show()

# ---------------------------------------------------------
plt.figure(figsize=(6,3))
plt.stackplot(range(1,8),
              df.groupby(['dow'])['casual_percentage'].mean(), 
              df.groupby(['dow'])['registered_percentage'].mean(), 
              labels=['Casual','Registered'])
plt.legend(loc='upper left')
plt.margins(0,0)
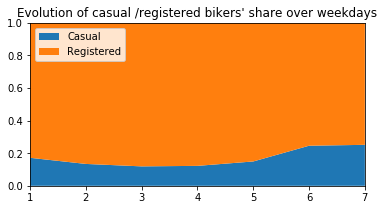
plt.title("Evolution of casual /registered bikers' share over weekdays")

# ---------------------------------------------------------
plt.figure(figsize=(6,6))
df_hours = pd.DataFrame(
    {"casual" : df.groupby(['dow'])['casual'].mean().values,
    "registered" : df.groupby(['dow'])['registered'].mean().values},
    index = df.groupby(['dow'])['casual'].mean().index)
df_hours.plot.bar(rot=0)
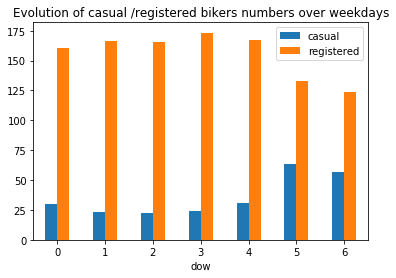
plt.title("Evolution of casual /registered bikers numbers over weekdays")

# ---------------------------------------------------------
plt.show()

<Figure size 432x432 with 0 Axes>

fig, ax = plt.subplots()
fig.set_size_inches(10, 8)
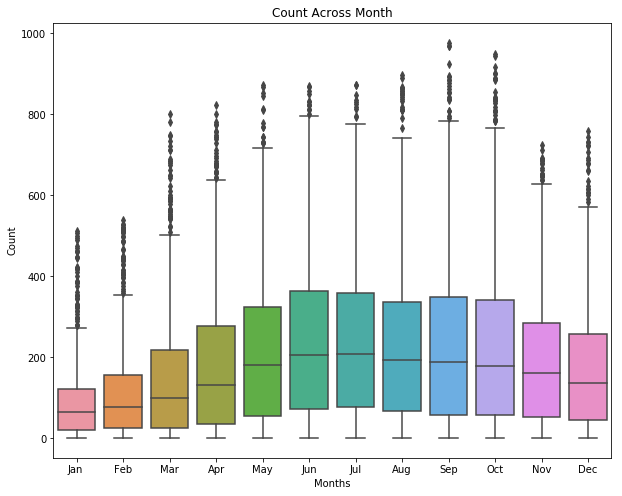
sns.boxplot(data=df, y="count", x="month_str", orient="v")
ax.set(xlabel="Months" , ylabel="Count", title="Count Across Month");

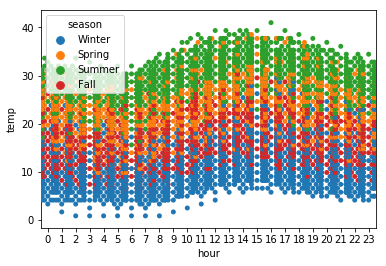
sns.swarmplot(x='hour', y='temp', data=df, hue='season')
plt.show()

# ---------------------------------------------------------
plt.figure(figsize=(6,3))
plt.stackplot(range(1,13),
              df.groupby(['month'])['casual_percentage'].mean(), 
              df.groupby(['month'])['registered_percentage'].mean(), 
              labels=['Casual','Registered'])
plt.legend(loc='upper left')
plt.margins(0,0)
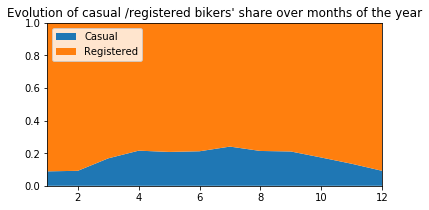
plt.title("Evolution of casual /registered bikers' share over months of the year")

# ---------------------------------------------------------
plt.figure(figsize=(6,6))
df_hours = pd.DataFrame(
    {"casual" : df.groupby(['month'])['casual'].mean().values,
    "registered" : df.groupby(['month'])['registered'].mean().values},
    index = df.groupby(['month'])['casual'].mean().index)
df_hours.plot.bar(rot=0)
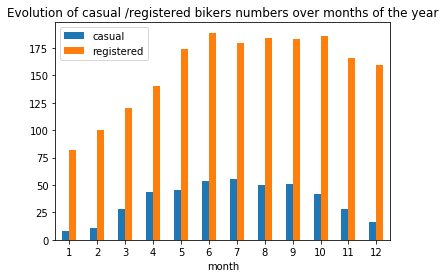
plt.title("Evolution of casual /registered bikers numbers over months of the year")

# ---------------------------------------------------------
plt.show()

<Figure size 432x432 with 0 Axes>

plt.figure(figsize=(10, 5))

bars = ['casual not on working days', 'casual on working days',\
        'registered not on working days', 'registered on working days',\
        'casual not on holidays', 'casual on holidays',\
        'registered not on holidays', 'registered on holidays']

qty = [df.groupby(['workingday'])['casual'].mean()[0], df.groupby(['workingday'])['casual'].mean()[1],\
      df.groupby(['workingday'])['registered'].mean()[0], df.groupby(['workingday'])['registered'].mean()[1],\
      df.groupby(['holiday'])['casual'].mean()[0], df.groupby(['holiday'])['casual'].mean()[1],\
      df.groupby(['holiday'])['registered'].mean()[0], df.groupby(['holiday'])['registered'].mean()[1]]

y_pos = np.arange(len(bars))
plt.barh(y_pos, qty, align='center')

plt.yticks(y_pos, labels=bars)
#plt.invert_yaxis()  # labels read top-to-bottom
plt.xlabel('Mean nb of bikers')
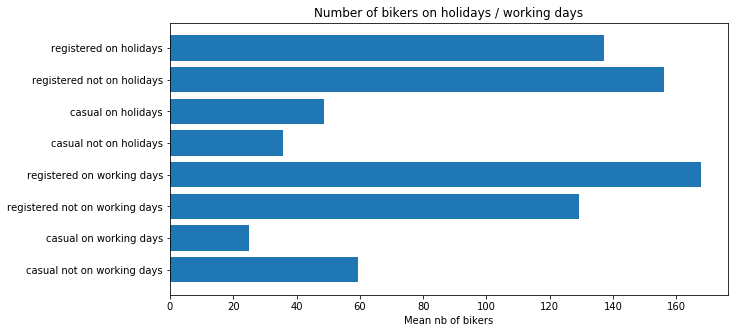
plt.title("Number of bikers on holidays / working days")
plt.show()

# ---------------------------------------------------------
plt.figure(figsize=(6,3))
plt.stackplot(range(1,5),
              df.groupby(['season'])['casual_percentage'].mean(), 
              df.groupby(['season'])['registered_percentage'].mean(), 
              labels=['Casual','Registered'])
plt.legend(loc='upper left')
plt.margins(0,0)
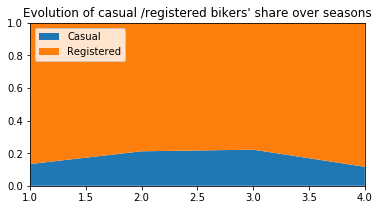
plt.title("Evolution of casual /registered bikers' share over seasons")

# ---------------------------------------------------------
plt.figure(figsize=(6,6))
df_hours = pd.DataFrame(
    {"casual" : df.groupby(['season'])['casual'].mean().values,
    "registered" : df.groupby(['season'])['registered'].mean().values},
    index = df.groupby(['season'])['casual'].mean().index)
df_hours.plot.bar(rot=0)
plt.title("Evolution of casual /registered bikers numbers over seasons")

# ---------------------------------------------------------
plt.show()

<Figure size 432x432 with 0 Axes>

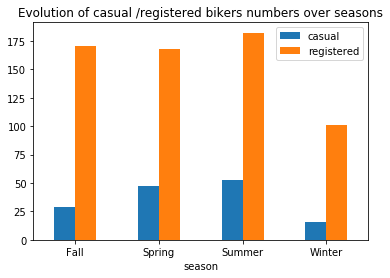
Generally speaking, the number of registered user increase between non working and working days where as the opposite can be seen when it comes to casual users (their number decrease between non working to working days). The spikes on the previous plots may corroborate this assumption because the registered users tend to use bike to go to work while casul users rent bike in the middle of the day…

Correlations

sns.set(style="white")

# Compute the correlation matrix
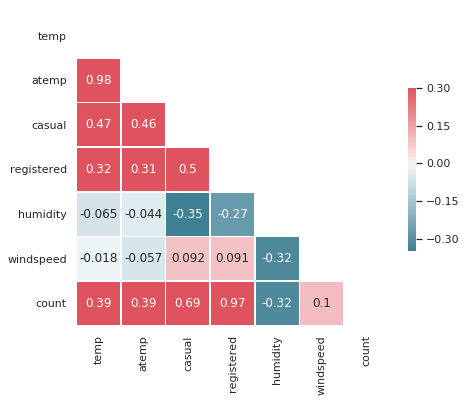
corr = df[["temp","atemp","casual","registered","humidity","windspeed","count"]].corr()

# Generate a mask for the upper triangle
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True

# Set up the matplotlib figure
f, ax = plt.subplots(figsize=(7, 6))

# Generate a custom diverging colormap
cmap = sns.diverging_palette(220, 10, as_cmap=True)

# Draw the heatmap with the mask and correct aspect ratio
sns.heatmap(corr, mask=mask, cmap=cmap, vmax=.3, center=0, annot=True,
            square=True, linewidths=.5, cbar_kws={"shrink": .5})

<matplotlib.axes._subplots.AxesSubplot at 0x7fa544b6bbe0>

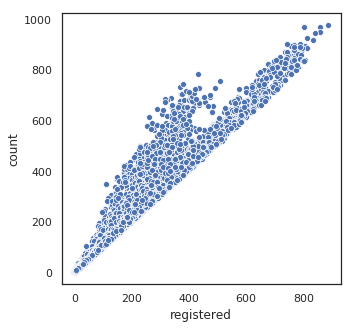
plt.figure(figsize=(5, 5))
sns.scatterplot(df.registered, df['count'])
plt.show()

Data preparation for models

# target 
y = (df["count"])

# drop irrelevant cols and target
cols_dropped = ["count", "datetime", "atemp", "month_str", "season", "dow_str", "weather_str",\
                "casual", "registered", "casual_percentage", "registered_percentage", "y_log", "Delta"] 
X = df.drop(columns=cols_dropped)
            
X.shape, y.shape

((10886, 11), (10886,))

y.head()

0    16
1    40
2    32
3    13
4     1
Name: count, dtype: int64

X.head()

	holiday	workingday	weather	temp	humidity	windspeed	dow	month	week	hour	year
0	0	0	1	9.84	81	0.0	5	1	52	0	2011
1	0	0	1	9.02	80	0.0	5	1	52	1	2011
2	0	0	1	9.02	80	0.0	5	1	52	2	2011
3	0	0	1	9.84	75	0.0	5	1	52	3	2011
4	0	0	1	9.84	75	0.0	5	1	52	4	2011

Split the data set into a training part and one for testing purpose.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

Features importance

def get_rmse(reg, model_name):
    """Print the score for the model passed in argument and retrun scores for the train/test sets"""
    
    y_train_pred, y_pred = reg.predict(X_train), reg.predict(X_test)
    rmse_train, rmse_test = np.sqrt(mean_squared_error(y_train, y_train_pred)), np.sqrt(mean_squared_error(y_test, y_pred))
    print(model_name, f'\t - RMSE on Training  = {rmse_train:.2f} / RMSE on Test = {rmse_test:.2f}')
    
    return rmse_train, rmse_test

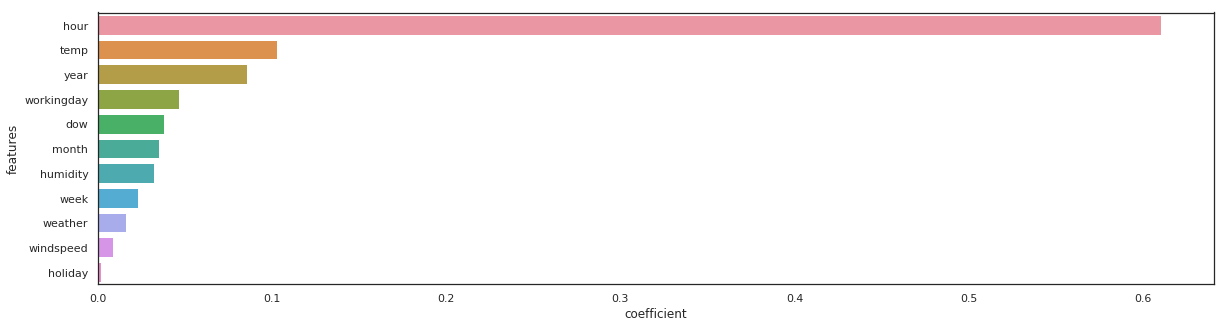
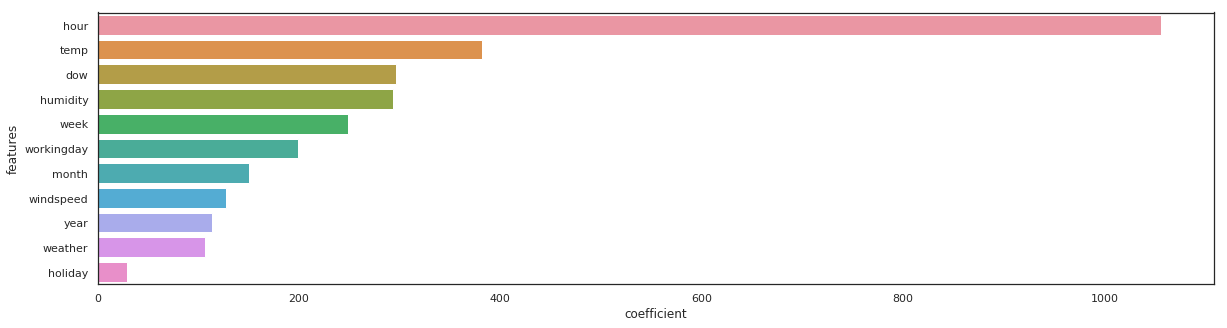
rf = RandomForestRegressor(n_estimators=100).fit(X_train, y_train)
_, _ = get_rmse(rf, 'rondom forrest')

features = pd.DataFrame()
features["features"] = X_train.columns
features["coefficient"] = rf.feature_importances_

features.sort_values(by=["coefficient"], ascending=False, inplace=True)
fig,ax= plt.subplots()
fig.set_size_inches(20,5)
sns.barplot(data=features, x="coefficient", y="features");

rondom forrest 	 - RMSE on Training  = 14.94 / RMSE on Test = 42.95

gb = GradientBoostingRegressor(n_estimators=100).fit(X_train, y_train)
_, _ = get_rmse(gb, 'gb')

features = pd.DataFrame()
features["features"] = X_train.columns
features["coefficient"] = gb.feature_importances_

features.sort_values(by=["coefficient"], ascending=False, inplace=True)
fig,ax= plt.subplots()
fig.set_size_inches(20,5)
sns.barplot(data=features, x="coefficient", y="features");

gb 	 - RMSE on Training  = 68.02 / RMSE on Test = 72.10

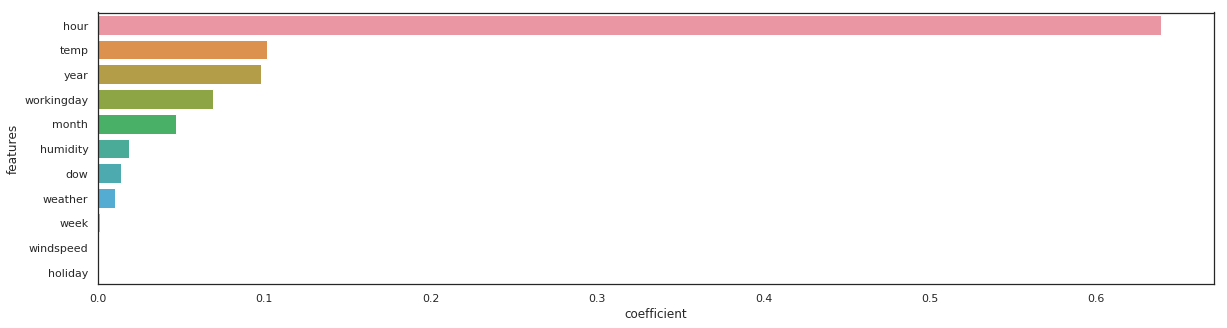
xgb_reg = xgb.XGBRegressor(n_estimators=100).fit(X_train, y_train)
_, _ = get_rmse(xgb_reg, 'xgb_reg')

features = pd.DataFrame()
features["features"] = X_train.columns
features["coefficient"] = xgb_reg.feature_importances_

features.sort_values(by=["coefficient"], ascending=False, inplace=True)
fig,ax= plt.subplots()
fig.set_size_inches(20,5)
sns.barplot(data=features, x="coefficient", y="features");

xgb_reg 	 - RMSE on Training  = 68.91 / RMSE on Test = 72.77

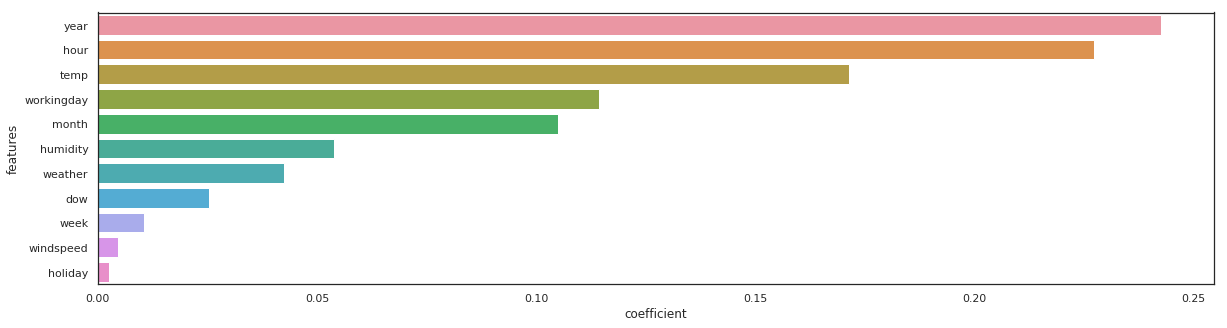
lgbm_reg = lgbm.LGBMRegressor(n_estimators=100).fit(X_train, y_train)
_, _ = get_rmse(lgbm_reg, 'lgbm_reg')

features = pd.DataFrame()
features["features"] = X_train.columns
features["coefficient"] = lgbm_reg.feature_importances_

features.sort_values(by=["coefficient"], ascending=False, inplace=True)
fig,ax= plt.subplots()
fig.set_size_inches(20,5)
sns.barplot(data=features, x="coefficient", y="features");

lgbm_reg 	 - RMSE on Training  = 31.57 / RMSE on Test = 40.24

The same feature come first, sometimes the order vary a little bit…

---

Models training and predictions

Metric - Root Mean Squared Error

Using logarithmic is an indirect way of measuring the performance of a loss function in terms of something more easily understandable

def rmsle(y, y_,convertExp=True):
    if convertExp:
        y = np.exp(y),
        y_ = np.exp(y_)
    log1 = np.nan_to_num(np.array([np.log(v + 1) for v in y]))
    log2 = np.nan_to_num(np.array([np.log(v + 1) for v in y_]))
    calc = (log1 - log2) ** 2
    return np.sqrt(np.mean(calc))

Please, also refer to the get_rmse function coded previously.

Base line & basic models

# list of all the basic models used at first
model_list = [
    LinearRegression(), Lasso(), Ridge(), ElasticNet(),
    RandomForestRegressor(), GradientBoostingRegressor(), ExtraTreesRegressor(),
    xgb.XGBRegressor(), lgbm.LGBMRegressor()
             ]

# creation of list of names and scores for the train / test
model_names = [str(m)[:str(m).index('(')] for m in model_list]
rmse_train, rmse_test = [], []

# fit and predict all models
for model, name in zip(model_list, model_names):
    model.fit(X_train, y_train)
    sc_train, sc_test = get_rmse(model, name)
    rmse_train.append(sc_train)
    rmse_test.append(sc_test)

LinearRegression 	 - RMSE on Training  = 140.53 / RMSE on Test = 146.52
Lasso 	 - RMSE on Training  = 140.57 / RMSE on Test = 146.59
Ridge 	 - RMSE on Training  = 140.53 / RMSE on Test = 146.52
ElasticNet 	 - RMSE on Training  = 143.30 / RMSE on Test = 149.20
RandomForestRegressor 	 - RMSE on Training  = 18.81 / RMSE on Test = 45.08
GradientBoostingRegressor 	 - RMSE on Training  = 68.02 / RMSE on Test = 72.10
ExtraTreesRegressor 	 - RMSE on Training  = 0.00 / RMSE on Test = 44.67
XGBRegressor 	 - RMSE on Training  = 68.91 / RMSE on Test = 72.77
LGBMRegressor 	 - RMSE on Training  = 31.57 / RMSE on Test = 40.24

Polynomial regression

from sklearn.preprocessing import PolynomialFeatures

poly_lin_reg = Pipeline([
    ("poly_feat", PolynomialFeatures(degree=3)),
    ("scaler", StandardScaler()),
    ("linear_reg", LinearRegression())
])

poly_lin_reg.fit(X_train, y_train)

sc_train, sc_test = get_rmse(poly_lin_reg, "Poly Linear Reg")

model_names.append('Poly Linear Reg')
rmse_train.append(sc_train)
rmse_test.append(sc_test)

Poly Linear Reg 	 - RMSE on Training  = 107.29 / RMSE on Test = 111.72

Hyperparameters tuning

Lasso

rd_cv = Ridge()
rd_params_ = {'max_iter':[1000, 2000, 3000],
                 'alpha':[0.1, 1, 2, 3, 4, 10, 30, 100, 200, 300, 400, 800, 900, 1000]}

rmsle_scorer = metrics.make_scorer(rmsle, greater_is_better=False)
rd_cv = GridSearchCV(rd_cv,
                  rd_params_,
                  scoring = rmsle_scorer,
                  cv=5)

rd_cv.fit(X_train, y_train)

GridSearchCV(cv=5, error_score='raise-deprecating',
       estimator=Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None,
   normalize=False, random_state=None, solver='auto', tol=0.001),
       fit_params=None, iid='warn', n_jobs=None,
       param_grid={'max_iter': [1000, 2000, 3000], 'alpha': [0.1, 1, 2, 3, 4, 10, 30, 100, 200, 300, 400, 800, 900, 1000]},
       pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
       scoring=make_scorer(rmsle, greater_is_better=False), verbose=0)

Lasso

sc_train, sc_test = get_rmse(rd_cv, "Ridge CV")

model_names.append('Ridge CV')
rmse_train.append(sc_train)
rmse_test.append(sc_test)

Ridge CV 	 - RMSE on Training  = 140.53 / RMSE on Test = 146.52

la_cv = Lasso()

alpha  = 1/np.array([0.1, 1, 2, 3, 4, 10, 30, 100, 200, 300, 400, 800, 900, 1000])
la_params = {'max_iter':[1000, 2000, 3000],'alpha':alpha}

la_cv = GridSearchCV(la_cv, la_params, scoring = rmsle_scorer, cv=5)
la_cv.fit(X_train, y_train).best_params_

{'alpha': 10.0, 'max_iter': 1000}

sc_train, sc_test = get_rmse(la_cv, "Lasso CV")

model_names.append('Lasso CV')
rmse_train.append(sc_train)
rmse_test.append(sc_test)

Lasso CV 	 - RMSE on Training  = 142.24 / RMSE on Test = 148.05

Knn regressor

knn_reg = KNeighborsRegressor()
knn_params = {'n_neighbors':[1, 2, 3, 4, 5, 6]}

knn_reg = GridSearchCV(knn_reg, knn_params, scoring = rmsle_scorer, cv=5)
knn_reg.fit(X_train, y_train).best_params_

{'n_neighbors': 1}

sc_train, sc_test = get_rmse(knn_reg, "kNN Reg")

model_names.append('kNN Reg')
rmse_train.append(sc_train)
rmse_test.append(sc_test)

kNN Reg 	 - RMSE on Training  = 0.00 / RMSE on Test = 140.08

LinearSVR

svm_reg = Pipeline([
    ("scaler", StandardScaler()),
    ("linear_svr", LinearSVR())
])

svm_reg.fit(X_train, y_train)

sc_train, sc_test = get_rmse(svm_reg, "SVM Reg")

model_names.append('SVM Reg')
rmse_train.append(sc_train)
rmse_test.append(sc_test)

SVM Reg 	 - RMSE on Training  = 146.86 / RMSE on Test = 153.43

Just for fun: a MLP (Multi Layer Perceptron)

I don’t expect this model to be reall efficient because it’s probably far too complex for our needs… but that’s just for fun!

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

X_train_, X_test_, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=0)

import tensorflow as tf

def model_five_layers(input_dim):

    model = tf.keras.models.Sequential()

    # Add the first Dense layers of 100 units with the input dimension
    model.add(tf.keras.layers.Dense(100, input_dim=input_dim, activation='sigmoid'))

    # Add four more layers of decreasing units
    model.add(tf.keras.layers.Dense(100, activation='sigmoid'))
    model.add(tf.keras.layers.Dense(100, activation='sigmoid'))
    model.add(tf.keras.layers.Dense(100, activation='sigmoid'))
    model.add(tf.keras.layers.Dense(100, activation='sigmoid'))

    # Add finally the output layer with one unit: the predicted result
    model.add(tf.keras.layers.Dense(1, activation='relu'))
    
    return model

model = model_five_layers(input_dim=X_train.shape[1])

# Compile the model with mean squared error (for regression)
model.compile(optimizer='SGD', loss='mean_squared_error')

# Now fit the model on XXX epoches with a batch size of XXX
# You can add the test/validation set into the fit: it will give insights on this dataset too
model.fit(X_train_, y_train, validation_data=(X_test_, y_test), epochs=200, batch_size=8)

WARNING:tensorflow:From /home/sunflowa/Anaconda/lib/python3.7/site-packages/tensorflow/python/ops/resource_variable_ops.py:435: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
WARNING:tensorflow:From /home/sunflowa/Anaconda/lib/python3.7/site-packages/tensorflow/python/keras/utils/losses_utils.py:170: to_float (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Train on 8708 samples, validate on 2178 samples
WARNING:tensorflow:From /home/sunflowa/Anaconda/lib/python3.7/site-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
Epoch 1/200
8708/8708 [==============================] - 1s 127us/sample - loss: 38212.8034 - val_loss: 37116.1185
Epoch 2/200
8708/8708 [==============================] - 1s 101us/sample - loss: 36155.7200 - val_loss: 30416.4880
Epoch 3/200
8708/8708 [==============================] - 1s 102us/sample - loss: 34061.7786 - val_loss: 33251.2080
Epoch 4/200
8708/8708 [==============================] - 1s 104us/sample - loss: 34448.0311 - val_loss: 33964.8975
Epoch 5/200
8708/8708 [==============================] - 1s 102us/sample - loss: 34450.1169 - val_loss: 35355.5311
7us/sample - loss: 35475.3280 - val_loss: 38654.4456

...

Epoch 195/200
8708/8708 [==============================] - 1s 95us/sample - loss: 35762.5541 - val_loss: 36520.5384
Epoch 196/200
8708/8708 [==============================] - 1s 97us/sample - loss: 35349.9739 - val_loss: 39536.0127
Epoch 197/200
8708/8708 [==============================] - 1s 95us/sample - loss: 35585.8599 - val_loss: 33362.7076
Epoch 198/200
8708/8708 [==============================] - 1s 95us/sample - loss: 35124.1187 - val_loss: 42101.3971
Epoch 199/200
8708/8708 [==============================] - 1s 96us/sample - loss: 35766.2078 - val_loss: 34425.0247
Epoch 200/200
8708/8708 [==============================] - 1s 93us/sample - loss: 35553.1240 - val_loss: 35824.4136





<tensorflow.python.keras.callbacks.History at 0x7fa53c534860>

y_train_pred, y_pred = model.predict(X_train_), model.predict(X_test_)
rmse_train_, rmse_test_ = np.sqrt(mean_squared_error(y_train, y_train_pred)), np.sqrt(mean_squared_error(y_test, y_pred))
print("MLP reg", f'\t - RMSE on Training  = {rmse_train_:.2f} / RMSE on Test = {rmse_test_:.2f}')

#sc_train, sc_test = get_rmse(model, "MLP reg")

model_names.append('MLP reg')
rmse_train.append(rmse_train_)
rmse_test.append(rmse_test_)

MLP reg 	 - RMSE on Training  = 188.90 / RMSE on Test = 189.27

---

Conclusion and submission

Before making a submission we have to choose the best model i.e with the smallest RMSE.

df_score = pd.DataFrame({'model_names' : model_names,
                         'rmse_train' : rmse_train,
                         'rmse_test' : rmse_test})
df_score = pd.melt(df_score, id_vars=['model_names'], value_vars=['rmse_train', 'rmse_test'])
df_score.head(10)

	model_names	variable	value
0	LinearRegression	rmse_train	140.527242
1	Lasso	rmse_train	140.566345
2	Ridge	rmse_train	140.527244
3	ElasticNet	rmse_train	143.301234
4	RandomForestRegressor	rmse_train	18.810298
5	GradientBoostingRegressor	rmse_train	68.017857
6	ExtraTreesRegressor	rmse_train	0.001515
7	XGBRegressor	rmse_train	68.907661
8	LGBMRegressor	rmse_train	31.570179
9	Poly Linear Reg	rmse_train	107.292639

plt.figure(figsize=(12, 10))
sns.barplot(y="model_names", x="value", hue="variable", data=df_score)

<matplotlib.axes._subplots.AxesSubplot at 0x7fa544c9af98>

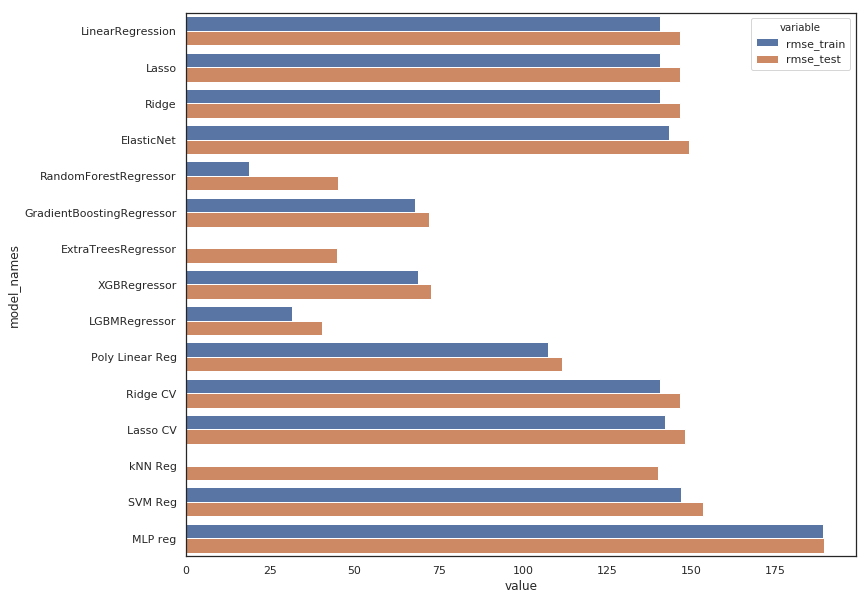
• The MLP model is indeed useless
• All linear regression have the same poor result, regularization using L1 or L2 with Lasso & Ridge doesn’t change anything which is quite obvious because those models are underfiting and need to be complexified (not regularized!). The same argument applies to ElasticNet which is a combinaison of the 2 above.
• Gridsearch don’t change anything because tuning regularization hyperparameters is not interesting for the same reason.
• The polynomial use help to improve results a little bit.
• Gradient Boosting & XGBoost Regressors are performing well without too overfitting.
• ExtraTree Regressor is out
• Random Forrest & LGBM Regressors are the best but the first one is clearly overfitting, so it would be better to choose the second one : LGBM Regressor

Now let’s see how do we have to sumbit our answer

y_sample = pd.read_csv("../input/sampleSubmission.csv")
y_sample.head()

	datetime	count
0	2011-01-20 00:00:00	0
1	2011-01-20 01:00:00	0
2	2011-01-20 02:00:00	0
3	2011-01-20 03:00:00	0
4	2011-01-20 04:00:00	0

df_test = pd.read_csv("../input/test.csv")
df_test = change_datetime(df_test)

# keep this col for the submission
datetimecol = df_test["datetime"]

test_cols_dropped = ['datetime',
 'atemp',
 'month_str',
 'season',
 'dow_str',
 'weather_str']

df_test = df_test.drop(columns=test_cols_dropped)
df_test.head()

	holiday	workingday	weather	temp	humidity	windspeed	dow	month	week	hour	year
0	0	1	1	10.66	56	26.0027	3	1	3	0	2011
1	0	1	1	10.66	56	0.0000	3	1	3	1	2011
2	0	1	1	10.66	56	0.0000	3	1	3	2	2011
3	0	1	1	10.66	56	11.0014	3	1	3	3	2011
4	0	1	1	10.66	56	11.0014	3	1	3	4	2011

We train our model on the whole data set (not only the splitted part). The more data we use, the better would be the results.

lgbm_reg = lgbm.LGBMRegressor()
lgbm_reg.fit(X, y)
y_pred_final = lgbm_reg.predict(df_test)

submission = pd.DataFrame({
        "datetime": datetimecol,
        "count": [max(0, x) for x in y_pred_final]
    })
submission.to_csv('bike_prediction_output.csv', index=False)

submission.head()

	datetime	count
0	2011-01-20 00:00:00	12.423966
1	2011-01-20 01:00:00	6.649667
2	2011-01-20 02:00:00	3.565470
3	2011-01-20 03:00:00	0.704959
4	2011-01-20 04:00:00	0.704959

Submit to kaggle, this model scores 0.41233. Not bad :)